Double-Iterative Gaussian Process Regression for Modeling Error Compensation in Autonomous Racing

Abstract

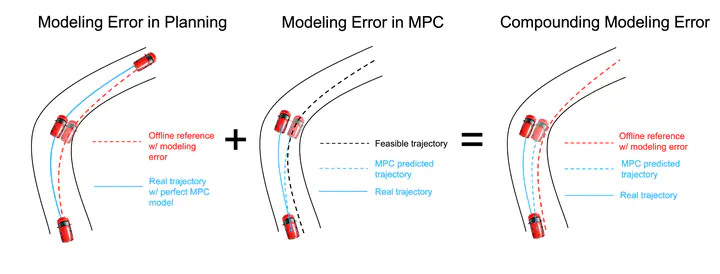
Autonomous racing control is a challenging research problem as vehicles are pushed to their limits of handling to achieve an optimal lap time; therefore, vehicles exhibit highly nonlinear and complex dynamics. Difficult-to-model effects, such as drifting, aerodynamics, chassis weight transfer, and suspension can lead to infeasible and suboptimal trajectories. While offline planning allows optimizing a full reference trajectory for the minimum lap time objective, such modeling discrepancies are particularly detrimental when using offline planning, as planning model errors compound with controller modeling errors. Gaussian Process Regression (GPR) can compensate for modeling errors. However, previous works primarily focus on modeling error in real-time control without consideration for how the model used in offline planning can affect the overall performance. In this work, we propose a \textit{double-GPR} error compensation algorithm to reduce model uncertainties; specifically we compensate both the planner’s model and controller’s model with two respective GPR-based error compensation functions. Furthermore we design an iterative framework to re-collect error-rich data using the racing control system. We test our method in the high-fidelity racing simulator Gran Turismo Sport (GTS); we find that our \textit{iterative, double-GPR} compensation functions improve racing performance and iteration stability in comparison to a single compensation function applied merely for real-time control.